Essa teoria foi elaborada e publicada pelo físico alemão Albert Einstein, que se baseou nos trabalhos de Hendrik Lorentz, Albert Michelson, Henri Poincaré (dentre outros) e compreende dois estudos inter-relacionados:
Relatividade Restrita (1905), que descreve os fenômenos espaçotemporais que ocorrem na ausência de gravidade;
Relatividade Geral (1915), que explica o funcionamento da gravidade, da física dos astros e da evolução do universo.
Teoria da Relatividade Restrita
A Teoria da Relatividade Restrita se aplica a Física do movimento, porém desconsiderando os efeitos de campos gravitacionais. É considerada uma “versão mais simplificada” da Teoria da Relatividade Geral, pois pode ser facilmente compreendida por todos. Normalmente, envolve cálculos relativamente simples, apesar de descrever fenômenos difíceis de serem aceitos pelo senso comum (PAULI, 2013). Ela é fundamentada em dois postulados:
Postulado 1
“As leis da Física são as mesmas em todos os referenciais inerciais.”
Certamente, a primeira pergunta a se fazer aqui é “o que é um referencial inercial?”. Mas antes, vamos definir o que é um referencial.
Um referencial é qualquer corpo que possa ser utilizado como orientação para que outro corpo se baseie no espaço (DISALLE, 2002). Por exemplo, imagine que um observador A esteja parado no chão no momento em que passa um trem. Imagine ainda que os observadores B e C estejam no trem.
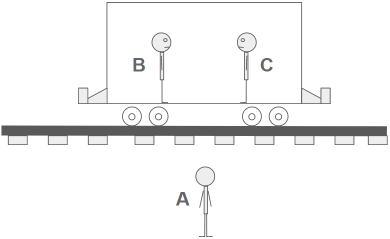
Imagem: Ciência Mundo
Para o observador A, o observador C está em movimento. Já para o observador B, o observador C está em repouso. Um referencial é o corpo onde um observador se encontra em repouso. Para o observador A, o referencial é o chão, mas para os observadores B e C o referencial é o trem. Então, na figura, nós temos dois referenciais, o trem que está se movendo e possui dois observadores (B e C), e o chão que está fixo e possui um observador (A).
Um referencial inercial é um tipo especial de referencial. Ele só pode estar, ou em repouso, ou em movimento retilíneo uniforme, mas nunca acelerando ou desacelerando. Ou seja, ele pode estar parado ou se movendo em linha reta com velocidade constante. Além disso, se um referencial se move com movimento linear uniforme em relação a um referencial inercial, então ele também será inercial (DISALLE, 2002).
Retornando ao primeiro postulado da Teoria da Relatividade Restrita, vemos que ele estabelece que esta teoria se aplica apenas a referenciais inerciais, daí o nome “restrita”. Além disso, determina também que diferentes referenciais inerciais compartilham as mesmas leis da Física. Ou seja, se você estiver dentro de uma nave espacial parada, e um amigo seu estiver dentro de uma nave se afastando em movimento linear uniforme de você, as leis da Física serão as mesmas!
Postulado 2
“A velocidade da luz é a mesma, quando medida a partir de qualquer referencial inercial.”
A velocidade da luz no vácuo é de 299.792.458 m/s! Normalmente, utilizamos valores arredondados para facilitar os cálculos como 300.000 km/s, ou 300 m/µs, ou simplesmente a letra “c”, muito utilizada na Física para representar essa grandeza. Ela é constante e independente tanto do movimento do emissor, quanto do movimento do referencial inercial de um observador! “Mas, como assim?! E se o emissor for uma pessoa com uma lanterna, viajando no mesmo sentido em que a luz viaja? A velocidade de deslocamento do emissor não seria somada à velocidade da luz?”. A resposta é NÃO! Não importa o quanto um emissor esteja “correndo”, a velocidade da luz será a mesma! Isso é algo muito difícil de se aceitar, mas é uma verdade no nosso universo. A velocidade da luz é constante, mesmo que o emissor ou o observador estejam em movimento (GREENE, 2001)!
Para compreendermos esse fenômeno, vamos imaginar a seguinte situação. Um observador A está na Terra, apontando uma lanterna para a estrela Próxima Centauri, a estrela mais próxima do sistema solar, a aproximadamente 4,24 anos-luz de distância. Para efeitos didáticos, vamos considerar que, tanto a Terra, quanto Próxima Centauri são referenciais inerciais e estão parados. Vamos desconsiderar também os efeitos da gravidade e da atmosfera, tanto da Terra, quanto da estrela.
Se o observador A fosse capaz de “ver” os fótons, ele os observaria se afastando a aproximadamente 300.000 km/s (velocidade da luz). Como Próxima Centauri está a 4,24 anos-luz de distância, conclui-se que, o observador A, teria que esperar 4,24 anos para que os fótons viajassem da Terra até a estrela. Bem simples, não?

Imagem: Ciência Mundo
Agora, vamos deixar as coisas mais divertidas. Imagine que o observador A está agora dentro de uma espaçonave, viajando em linha reta para Próxima Centauri, a 99% da velocidade da luz. Para ele, que está viajando, nada mudou. Tudo está acontecendo do mesmo jeito. Além disso, se ele não tiver como verificar um referencial externo, sequer saberá que está viajando. Se ele apontar uma lanterna para Próxima Centauri, continuará a “ver” fótons se afastando a 300.000 km/s. Se a espaçonave está se movendo a 99% da velocidade da luz, estariam esses fótons viajando a quase 2 vezes a velocidade da luz? Mas como isso seria possível, se a velocidade da luz é a maior velocidade do nosso universo? A resposta está no observador B, que ficou estacionado na Terra enquanto o observador A viajava.
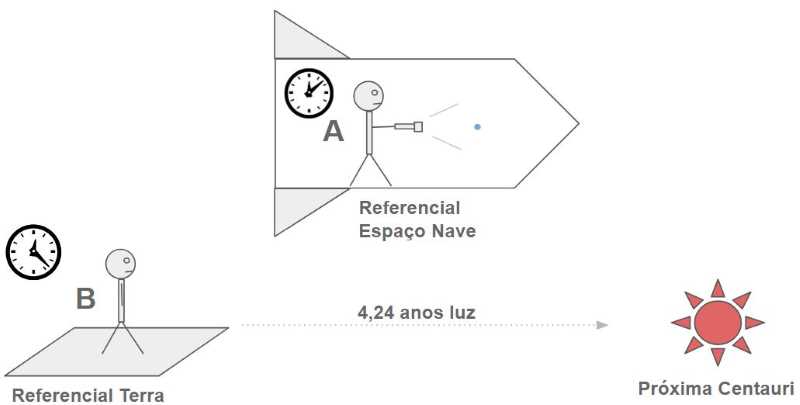
Imagem: Ciência Mundo
Para o observador B os fótons que saem da lanterna do observador A continuam a viajar pelo espaço, na mesma velocidade que viajariam se tivessem sido emitidos da Terra, ou seja, a 300.000 km/s. Porém, na visão do observador B, algo muito estranho está acontecendo dentro da nave! Os fótons não estão se afastando do Observador A à 300.000 km/s, mas sim a aproximadamente 3.000 km/s, ou seja, 1% da velocidade da luz! Além disso, as coisas estão em “câmera lenta” dentro da nave, se compararmos com a velocidade cotidiana da terra. O tempo na nave dilatou! Esse efeito é chamado de dilatação temporal.
Isso acontece porque a física do nosso universo parece “esticar” o tempo dos viajantes para garantir que a velocidade da luz seja a mesma velocidade máxima em qualquer referencial inercial. Assim, qualquer corpo viajando a uma velocidade inferior à velocidade da luz terá sua experiência temporal ajustada para garantir conformidade com esse fenômeno relativístico. Essa dilatação temporal nunca é percebida pelo viajante.
A dilatação temporal tem uma implicação assombrosa. Os dois observadores estão experimentando o tempo em ritmos diferentes. Imagine que os observadores A e B sejam irmãos gêmeos com 20 anos de idade, e que o observador A tenha ganho um prêmio onde ele irá viajar por 10 anos dentro de uma nave espacial, a 80% da velocidade da luz. Quando o observador A retornar, terão passados 10 anos dentro da nave, e 16,7 anos aqui na Terra! O observador A terá 30 anos, enquanto o observador B terá 36,7 anos. Esse é o famoso efeito conhecido na Física como o paradoxo dos gêmeos (NERLICH, 2004).
Além disso, há outro efeito acontecendo, que ainda não mencionamos. Para o observador A, a espaçonave está encolhendo, no mesmo sentido em que ela viaja. Isso acontece porque os copos diminuem seus comprimentos quando viajam em velocidades próximas à da luz. Observe que isso é apenas uma percepção relativística que só é notada pelo observador que está “estacionado” em relação a algo que viaja. O viajante não sente absolutamente nada. Seu ambiente, ou referencial inercial, continua o mesmo de quando ele estava parado.
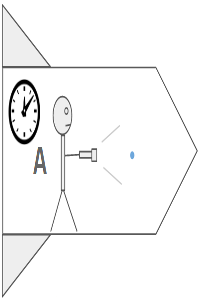
Imagem: Ciência Mundo
Outra implicação muito estranha está relacionada a “como a luz percebe o tempo”. As fórmulas da teoria da relatividade nos mostram que é impossível para um corpo com massa viajar a velocidade da luz, pois seria necessário uma quantidade infinita de energia para tal feito. Contudo, apenas para matar a curiosidade e entendermos como seria viajar a velocidade da luz, vamos imaginar que o Observador A está viajando a 300.000 Km/s! Nesse cenário, os fótons que saem da lanterna estão à velocidade da luz, mas ele também está! Como a teoria da relatividade restrita nos garante que as leis da física são as mesmas em todos os referenciais inerciais, nada diferente pode estar acontecendo dentro da nave. Ele certamente, estará ainda vendo os fótons viajando a 300.000 Km/s. Mas como isso é possível? Acontece que o observador A chegou ao seu destino instantaneamente! Como ele estava viajando na mesma velocidade dos fótons que saem da lanterna, não foi possível vê-los se distanciar! Ele ficou congelado naquele momento durante toda viagem, parado segurando a lanterna, atrás dos fótons, que só se distanciaram quando ele chegou ao seu destino. A dilatação temporal foi máxima, pois o tempo não passou para ele! Ou seja, o tempo não passa para algo que esteja a velocidade da luz. No entanto, essa velocidade só pode ser alcançada por partículas sem massa. Por exemplo, no vácuo o fóton não experimenta o tempo!
Teoria da Relatividade Geral
A Teoria da Relatividade Restrita, descrita anteriormente, foi um grande avanço para a Física no início do século XX, mas ela se limitava a descrever fenômenos apenas na ausência de gravidade. Isso era uma grande limitação para sua aplicação no mundo real, já que vivemos em um universo caótico em que a gravidade atua sobre tudo! Assim, logo após a publicação da relatividade restrita, Einstein começou a investigar esse novo “ator” que deveria ser considerado nas fórmulas da relatividade. Contudo, logo no início, ele já esbarrou em um problema! Suas ideias começaram a entrar em conflito com os pressupostos de Isaac Newton, que era considerado o “pai” da Física na época.
Segundo Newton, a órbita dos corpos ao redor de planetas, como a Lua, por exemplo, era o resultado da “força” da gravidade puxando esses corpos para “baixo” enquanto eles tendem a ir para frente, dando assim estabilidade de movimento orbital. Ele costumava a utilizar como exemplo um canhão imaginário para explicar tal fenômeno (PESNELL, 2018). Observe a figura abaixo e imagine um canhão atirando uma bala (ou bola de ferro) em algum lugar do planeta. Certamente, essa bala cairá em algum ponto A à sua frente. Se colocarmos mais pólvora nesse canhão, certamente a bala cairá mais à frente ainda em um ponto B. Segundo Newton, se colocarmos uma quantidade exata de pólvora, considerando a massa da bala e a velocidade necessária, seria possível fazer essa bala entrar em órbita (C na figura), girando eternamente ao redor da terra, ou até encontrar um obstáculo. Colocando mais pólvora ainda, essa bala atingiria velocidade suficiente para o escape gravitacional (D na figura).
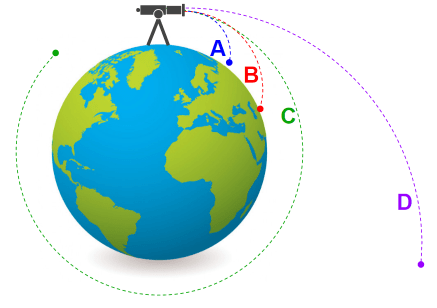
Imagem: Ciência Mundo / Pixabay
Ainda, segundo Newton, essa “força”, que ele chamava de gravidade, dependia apenas da massa dos corpos, e agia instantaneamente no universo. Para ele, se o sol desaparecesse agora, todos os planetas que anteriormente o orbitavam, passariam a vagar por inércia instantaneamente pelo espaço. Foi nesse momento que a Teoria da Gravitação Universal de Newton e a Teoria da Relatividade entraram em conflito. Einstein já havia estabelecido em seu primeiro postulado da relatividade restrita em 1905 que a velocidade da luz era a maior velocidade do universo. Logo, como poderia a gravidade ser instantânea? Além disso, como ele já estava desconfiado de que a gravidade atuava também em partículas sem massa (como fótons), então a definição newtoniana de que a gravidade seria uma força parecia estar errada.
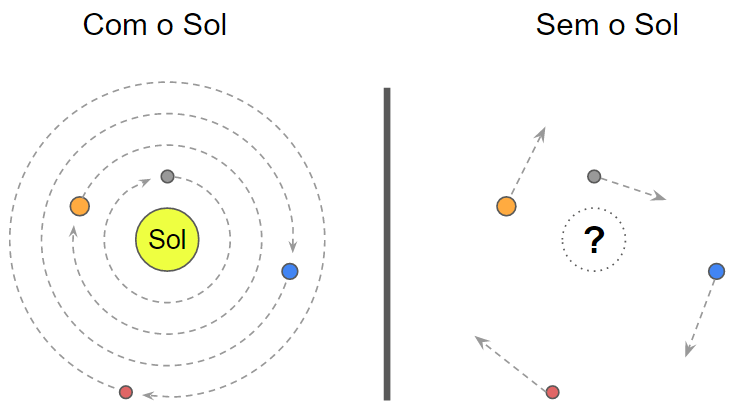
Imagem: Ciência Mundo
Foi então que, através de um experimento mental, Einstein teve o que ele chamou de “o pensamento mais feliz de sua vida” (MEDEIROS, 2005). Ele imaginou uma pessoa em cima de uma balança, ambos dentro de uma caixa. Neste cenário, a balança está marcando o peso da pessoa normalmente. Ele então começou a avaliar em que situações isso seria possível. Primeiro ele verificou que isso seria correto se a caixa estivesse estática, na superfície terrestre. Depois, ele verificou que isso também seria possível se a caixa fosse o interior de uma espaçonave, longe de campos gravitacionais, acelerando a 9,8 m/s2. Ele então percebeu que as duas situações eram equivalentes, e que nenhum experimento que a pessoa fizesse dentro da caixa seria capaz de determinar se ela está na Terra, ou acelerando no espaço.
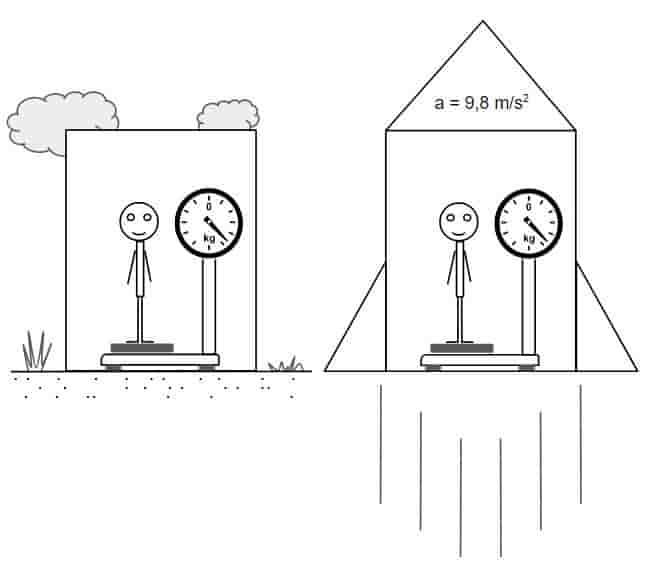
Imagem: Ciência Mundo
Einstein então, em um segundo experimento mental, imaginou o que aconteceria, se a caixa fosse um elevador na Terra e seu cabo se soltasse. Nessa situação, tudo o que está dentro do elevador cairia junto com ele. A pessoa não sentiria mais o seu peso, e teria a sensação de flutuar junto com o elevador e a balança, que, nesse caso, estaria marcando 0 kg. Ele então verificou que esta seria a mesma sensação que a pessoa teria se a caixa fosse uma espaçonave flutuando em inércia no vazio do espaço, pois nesse caso ela também não sentiria o seu peso. Contudo, no primeiro caso, onde a caixa (elevador) está em queda livre, a gravidade e a aceleração estão se cancelando. Já no segundo caso, onde a caixa (espaçonave) está vagando pelo espaço, a gravidade não existe. Ele percebeu, mais uma vez, que seria impossível para uma pessoa dentro de uma dessas caixas, determinar se ela está em um elevador caindo ou em uma espaçonave flutuando no vazio.
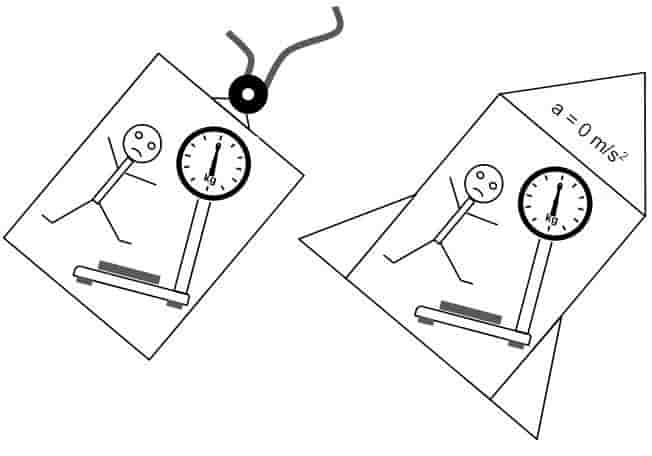
Imagem: Ciência Mundo
Após realizar os dois experimentos mentais, Einstein concluiu haver uma relação muito forte entre gravidade e aceleração, a ponto de ser impossível distinguir uma coisa da outra. Ele chamou esse fenômeno de princípio da equivalência, e estabeleceu que gravidade é aceleração, sem o envolvimento de forças (GREENE, 2001). Mas, o que causa essa aceleração?
Einstein descobriu um comportamento muito estranho do nosso universo. A simples presença de um corpo com massa causa alterações na geometria do espaço ao seu redor (ECKHARDT, 2019). Em outras palavras, a gravidade é como um “mapa”, criado por corpos com massa, que mostra como outros corpos devem se mover em sua presença. O que observamos nas órbitas e nas alterações de movimento de objetos no espaço, não é a atuação de uma força, mas sim um comportamento que os corpos exibem ao andar em um espaço curvo. Por exemplo, se pudéssemos acompanhar um asteroide vagando pelo espaço, perceberíamos que ele está tentando seguir a sua trajetória em linha reta, mas é obrigado a obedecer às curvas do espaço que são criadas por outros objetos massivos como planetas e estrelas. No entanto, devemos observar também que corpos vagando pelo espaço, não só obedecem à curvatura criada por outros corpos, mas também criam sua própria curvatura ao seu redor. Por exemplo, planetas na órbita de uma estrela, também podem possuir luas em suas próprias órbitas. Assim, a matéria diz para o espaço como se curvar, e o espaço diz para a matéria como se mover.

Imagem: Pixabay
Devemos notar ainda que, se o espaço e o tempo estão interligados, e a gravidade pode ser interpretada como a curvatura do espaço, então a gravidade também influi na passagem do tempo. Nesse caso, quanto mais forte for o campo gravitacional, mais devagar passará o tempo. Esse fenômeno é chamado de dilatação temporal gravitacional, e é similar àquela dilatação temporal causada por movimento, que vimos na relatividade restrita, mas dessa vez, a diferença temporal é causada pela gravidade de um corpo massivo próximo. Por exemplo, um relógio na superfície do Sol, que possui gravidade igual a 274 m/s², andaria mais devagar do que um relógio na Terra, que possui gravidade igual a 9,8 m/s² (CHOU, 2010).
Retornando a Teoria da Gravitação Universal de Newton, vemos que ela tinha alguns equívocos, que foram esclarecidos com a Teoria da Relatividade Geral. Inicialmente, a gravidade não é uma força, mas sim uma deformação no tecido do espaço-tempo, causada pela presença de corpos com massa. Além disso, ela não se propaga instantaneamente, mas sim através de ondas gravitacionais que viajam próximas da velocidade da luz. Logo, se o sol deixasse de existir agora, levaria cerca de 8 min, até que a Terra deixasse de ter sua influência gravitacional. E por fim, partículas que não possuem massa (como fótons, por exemplo) também sofrem perturbações gravitacionais, pois a gravidade atua alterando o caminho por onde passam os corpos, e não como uma força nos corpos em si. Essa curvatura na trajetória dos fótons (ou da luz) pode ser comprovada em um eclipse solar, onde percebemos que a imagem das estrelas visualmente próximas ao Sol tem suas posições levemente deslocadas para fora, se compararmos com a mesma imagem das estrelas na ausência do Sol. Algumas dessas estrelas deveriam, inclusive, estar invisíveis, pois estão, na verdade, atrás do Sol. Um dos primeiros registros desse fenômeno ocorreu no Brasil, no eclipse do dia 29 de maio de 1919, na cidade de Sobral – CE (DE OLIVEIRA, 1919).
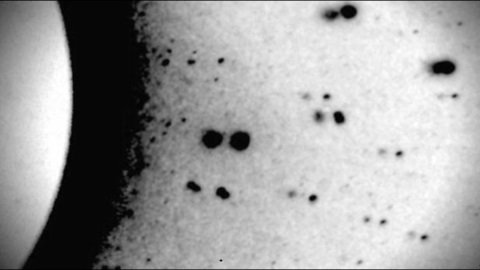
Comprovação da curvatura da trajetória da luz, Sobral – CE.
Imagem: Pixabay
Os estudos de Einstein serviram de suporte para que outro físico, chamado Karl Schwarzschild, previsse a existência de uma entidade espantosa em nosso universo: o buraco negro. Apesar de nada poder ser mais rápido do que a luz, Schwarzschild percebeu que um corpo supermassivo poderia criar uma curva tão acentuada no espaço, e consequentemente, um campo gravitacional tão intenso, que seria como uma armadilha relativística, da onde nem mesmo a luz escaparia. Ele previu que esses corpos seriam como pontos negros no céu, que só poderiam ser identificados através da sua interação com outros astros ao seu redor. Schwarzschild nunca viu um buraco negro, mas quando analisava as fórmulas de Einstein, percebia que a existência deles era uma consequência lógica da Teoria da Relatividade Geral. Hoje, sabemos que esses corpos existem, e são naturalmente formados ao final da vida de estrelas supermassivas (FLORIANO, 2020).

Imagem: Pixabay
Historicamente, a Teoria da Relatividade Geral foi uma das maiores contribuições de um único cientista para a compreensão do funcionamento do nosso universo. Contudo, quando ela foi publicada, em 1915, não foi assimilada rapidamente pela sociedade da época. Estima-se que, no mundo, não haviam 10 pessoas que compreendessem o que Einstein estava tentando explicar em seu trabalho. Assim, apesar dessa teoria ter sido confirmada no eclipse de 1919, seus fundamentos só se tornaram consolidados na Física teórica e na Astronomia a partir da década de 60, que é considerada a “era de ouro” da relatividade geral. Einstein faleceu um pouco antes disso, em 18 de abril de 1955.
Vídeos Relacionados
Vídeo: Canal “Ciência todo dia” em Youtube.
Vídeo: Canal “BBC News Brasil” em Youtube.
Ficção e documentários relacionados
A História de Albert Einstein – History Channel
Documentário do History Channel sobre Albert Einstein (1879-1955), e a elaboração das teorias da relatividade. <Link>
Referências
CHOU, Chin-Wen et al. Optical clocks and relativity. Science, v. 329, n. 5999, p. 1630-1633, 2010.
DE OLIVEIRA, José Carlos Teixeira. Centenário da Comprovação Experimental da Teoria da Relatividade Geral de Albert Einstein através do Eclipse Solar Total de 1919 em Sobral.
DISALLE, Robert. Space and time: Inertial frames. 2002.
ECKHARDT, Gustavo et al. FÍSICA PARA TODOS: UM EXPERIMENTO SOBRE GRAVIDADE. Salão do Conhecimento, 2019.
FLORIANO, Tiago Cardoso. Introdução aos buracos negros. 2020.
GREENE, Brian. O universo elegante: supercordas, dimensões ocultas e a busca da teoria definitiva. Companhia das Letras, São Paulo, 2001.
MEDEIROS, Alexandre; DE MEDEIROS, Cleide Farias. Einstein, a física dos brinquedos e o princípio da equivalência. Caderno Brasileiro de Ensino de Física, v. 22, n. 3, p. 299-315, 2005.
NERLICH, Graham. How the twins do it: STR and the clock paradox. Analysis, v. 64, n. 1, p. 21-29, 2004.
PAULI, Wolfgang. Theory of relativity. Courier Corporation, 2013.
PESNELL, W. Dean. The flight of Newton’s cannonball. American Journal of Physics, v. 86, n. 5, p. 338-343, 2018.
Cite-nos
SANTOS, Gabriel. Teoria da relatividade – Uma breve introdução. Ciência Mundo, Rio de Janeiro, mar. 2021. Disponível em: . Acesso em: .

















